演習 03
問題 1
アルファベット小文字からなる文字列 s を受け取り、母音(a, e, i, o, u)を取り除いた子音のみの文字列をコンソールに表示する関数 printConsonant を作成して以下のプログラムを完成させよ。
// ここに自作関数を作る
void setup() {
noLoop();
}
void draw() {
String[] words = {
"racoon",
"dog",
"rabbit",
"cow",
"horse",
"hippopotamus",
};
for (int i = 0; i < words.length; ++i) {
printConsonant(words[i]);
}
}
実行結果
rcn
dg
rbbt
cw
hrs
hppptms
問題 2
自然数 について、 を満たす自然数 が存在するとき、 を立方数(cubic number)と呼ぶ。 また、そのときの を の三乗根(cubic root)と呼ぶ。
1 以上の整数値 y を受け取り、y が立方数であればその三乗根をかえし、そうでなければ -1 を返す関数 cubicRoot を作成して以下のプログラムを完成させよ。
// ここに自作関数を作る
void setup() {
noLoop();
}
void draw() {
int[] numbers = {1, 8, 100, 3375, 9999, 997002999};
for (int i = 0; i < numbers.length; ++i) {
int c = cubicRoot(numbers[i]);
if (c < 0) {
println(numbers[i] + " is not a cubic number");
} else {
println("cubic root of " + numbers[i] + " is " + c);
}
}
}
実行結果
cubic root of 1 is 1
cubic root of 8 is 2
100 is not a cubic number
cubic root of 3375 is 15
9999 is not a cubic number
cubic root of 997002999 is 999
問題 3
色 について、 とすると、の補色は によって求められる。
整数値 r、g、b を受け取り、 その補色を計算する関数 complementaryColor を作成して以下のプログラムを完成させよ。
complementaryColor の戻り値には color 型を使用すると良い。
// ここに自作関数を作る
void setup() {
size(400, 200);
}
void draw() {
background(255);
int r = 51;
int g = 153;
int b = 0;
color c1 = color(r, g, b);
color c2 = complementaryColor(r, g, b);
noStroke();
fill(c1);
ellipse(100, 100, 200, 200);
fill(c2);
ellipse(300, 100, 200, 200);
}
実行結果

問題 4
小文字のアルファベットをランダムに返す関数 randomChar を作成して以下のプログラムを完成させよ。
// ここに自作関数を作る
void setup() {
noLoop();
}
void draw() {
String s = "";
for (int i = 0; i < 50; ++i) {
s += randomChar();
}
println(s);
}
実行結果の例
mjrbkskrpxgmmetpsnflwjmzzkjciiflnhasunhepxqkxkxcdv
問題 5
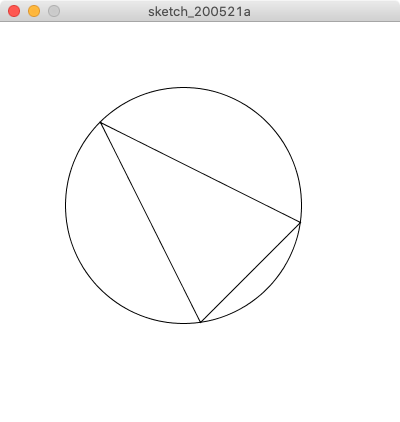
3 点 A = (x1, y1), B = (x2, y2), C = (x3, y3) を結ぶ三角形とその外接円を描画する関数 drawCircumscribedCircle を作成して以下のプログラムを完成させよ。
x1, y1, x2, y2, x3, y3 は実数値として与えられる。
外接円の中心は線分 AB, AC, BC の垂直二等分線の交点である。 また、点 A, B, C は外接円の円周上にある。
以下の intersection 関数と verticalBisector 関数を利用して良い。
/**
* 二直線 y = a1 x + b1, y = a2 x + b2 の交点 (x, y) を持った2要素の実数配列を返す
*/
float[] intersection(float a1, float b1, float a2, float b2) {
float x = - (b1 - b2) / (a1 - a2);
float y = a1 * x + b1;
float[] xy = {x, y};
return xy;
}
/**
* 点 (x1, y1) と点 (x2, y2) を結ぶ線分の垂直二等分線 y = ax + b の(a, b) を持った2要素の実数配列を返す
*/
float[] verticalBisector(float x1, float y1, float x2, float y2) {
float mx = (x1 + x2) / 2;
float my = (y1 + y2) / 2;
float a = -(x1 - x2) / (y1 - y2);
float b = my - a * mx;
float[] ab = {a, b};
return ab;
}
// ここに自作関数を作る
void setup() {
size(400, 400);
}
void draw() {
background(255);
drawCircumscribedCircle(100, 100, 300, 200, 200, 300);
}
実行結果