演習

問題 1

整数配列 $a$ の先頭から $k$ 個の要素の総和を求める関数は以下のように再帰的に定義できる。

$\begin{align} f(a, k) = \begin{cases} 0 & (k=0) \\ a[k - 1] + f(a, k - 1) & (k > 0) \end{cases} \end{align}$

この関数を再帰を用いて作成し、整数配列の総和を計算するプログラムを作成せよ。

問題 2

ヒープソートにおける siftup 関数は以下のように再帰的に定義できる。

siftup(data, i):
  もし i番の頂点が根ではない かつ i番の頂点の値がparent(i)番の頂点の値より大きい ならば、
  i番の頂点の値とparent(i)番の頂点の値を入れ替えてsiftup(data, parent(i))を実行する

ヒープソートのプログラムの siftup 関数を、上記の定義に基づいて、再帰を用いて再作成せよ。

問題 3

ヒープソートにおける siftdown 関数は以下のように再帰的に定義できる。

siftdown(data, n, i)
  もし i番の頂点が子を持つ かつ i番の頂点の値がgreaterChild(i)番の頂点の値より小さい ならば
  i番の頂点の値とgreaterChild(i)番の頂点の値を入れ替えてsiftdown(data, n, greaterChild(i))を実行する

ヒープソートのプログラムの siftdown 関数を、上記の定義に基づいて、再帰を用いて再作成せよ。 siftdown に新しい引数が増えていることに注意すること。根から siftdown をする場合には、siftdown(data, n, 0) と呼び出す。

問題 4

$\text{linearSearch}(a, k, t)$ は、 $a[i] == t$ となる $i (k \leq i < |a|)$ が存在するとき $i$ を、そうでないとき $-1$ を返す関数である。ただし $|a|$ を $a$ の要素数とする。 $\text{linearSearch}(a, k, t)$ は、次のように再帰的に定義できる。

$\begin{align} \text{linearSearch}(a, k, t) = \begin{cases} -1 & (k = |a|) \\ k & (t = a[k]) \\ \text{linearSearch}(a, k + 1, t) & (\text{otherwise}) \end{cases} \end{align}$

この関数を再帰を用いて作成し、線形探索を行う以下のプログラムを完成させよ。

void setup() {
  noLoop();
}

void draw() {
  int[] data = {5, 9, 23, 26, 55, 66, 79, 80, 82, 93};
  find(data, 0);
  find(data, 5);
  find(data, 50);
  find(data, 55);
  find(data, 93);
  find(data, 100);
}

void find(int[] data, int target) {
  int index = linearSearch(data, 0, target);
  if (index > -1) {
    println("Found: data[" + index + "] == " + target);
  } else {
    println("Not Found: " + target);
  }
}

問題 5

配列 data の先頭 n 要素をバブルソートする関数 bubbleSort(data, n) は以下のように再帰的に定義できる。

bubbleSort(data, n)
  もし n が 0 より大きければ以下を実行する
    i を 1 とする
    i が n より小さい間以下を実行する
      もし data[i - 1] > data[i] であれば data[i - 1] と data[i] を入れ替える
      i を 1 増やす
    bubbleSort(data, n - 1) を実行する

この関数を再帰を用いて作成し、バブルソートを行う以下のプログラムを完成させよ。

void setup() {
  noLoop();
}

void draw() {
  int[] data = generateData(20);

  println("before sort");
  printArray(data);

  bubbleSort(data, data.length);

  println("after sort");
  printArray(data);

  if (isSorted(data)) {
    println("OK");
  } else {
    println("NG");
  }
}

int[] generateData(int n) {
  int[] result = new int[n];
  for (int i = 0; i < n; ++i) {
    result[i] = int(random(50000));
  }
  return result;
}

boolean isSorted(int[] data) {
  for (int i = 1; i < data.length; ++i) {
    if (data[i - 1] > data[i]) {
      return false;
    }
  }
  return true;
}

問題 6

バブルソートのプログラムを再帰を用いずに作成せよ。

問題 7

再帰を用いたバブルソートのプログラムにおいて、ソートする配列の要素数を 20000 で実行した時にどうなるか確認せよ。

問題 8

Fibonacci 数列の第 $n$ 項 $\text{fibonacci}(n)$ は以下のように定義される。

$\begin{align} \text{fibonacci}(n) = \begin{cases} 0 & (n = 0 ) \\ 1 & (n = 1 ) \\ \text{fibonacci}(n - 1) + \text{fibonacci}(n - 2) & \text{otherwise} \end{cases} \end{align}$

Fibonacci 数列の第 n 項を計算する関数 fibonacci を再帰を用いずに作成し、次のプログラムを完成させよ。

void setup() {
  noLoop();
}

void draw() {
  for (int i = 0; i <= 10; ++i) {
    println("fibonacci(" + i + ") = " + fibonacci(i));
  }
}

問題 9

Fibonacci 数列の第 n 項を計算する関数 fibonacci を再帰を用いて作成し、次のプログラムを完成させよ。

void setup() {
  noLoop();
}

void draw() {
  for (int i = 0; i <= 10; ++i) {
    println("fibonacci(" + i + ") = " + fibonacci(i));
  }
}

問題 10

再帰を用いて作成した fibonacci 関数を用いて、fibonacci(40)を計算せよ。その際に、fibonacci 関数が呼び出された回数と、計算にかかった時間を出力せよ。 fibonacci 関数の呼び出し回数はグローバル変数を用いて数えるとよい。計算にかかった時間は millis 関数を用いて計算する。 millis 関数は、プログラムの実行時からmillis関数を呼び出した瞬間までに何ミリ秒経過したかを返す。

問題 11

要素数 100 の int 型配列 cache をグローバル変数として宣言し、既に計算した fibonacci(n)の値を cache[n] に格納することで前問のプログラムの効率化を行う。ここで、cache[n] が 0 であれば fibonacci(n)は未計算であり、cache[n]が 0 より大きければ計算済みとなるようにデータを格納せよ。前問のプログラムと呼び出し回数および計算時間を比較せよ。

問題 12

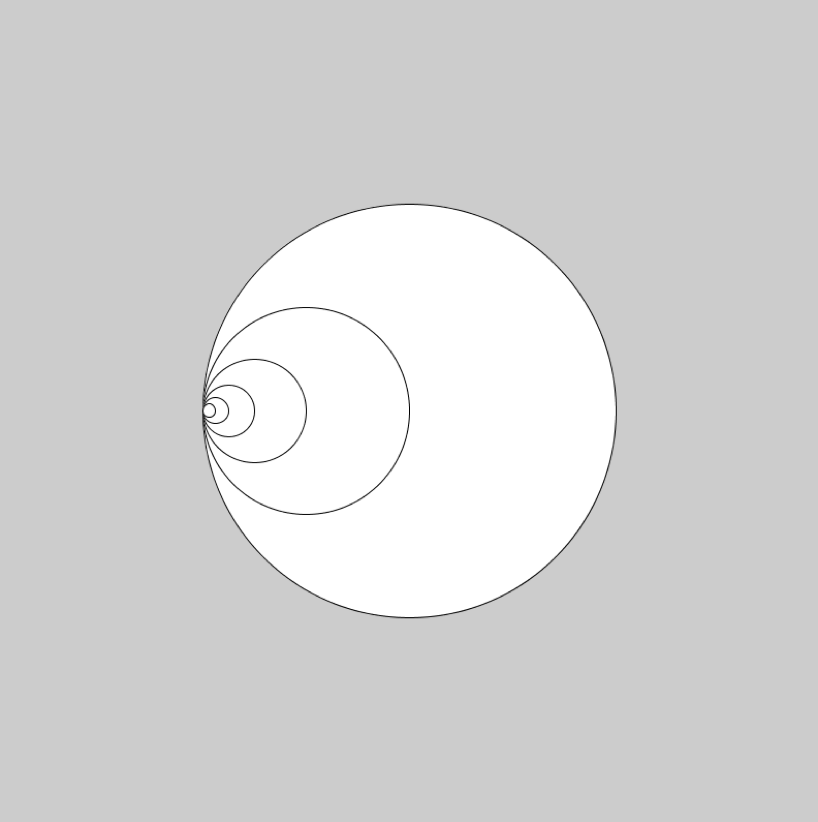
再帰関数を用いて下記の描画結果が得られるプログラムを作成せよ。

Window サイズは横 800，縦 800
各円の中心の y 座標は同じで，各円同士は円の左端で接している
一番外側の円の直径は Window の 1 辺の半分の長さ
外側から n 番目の円の直径は n-1 番目の円の直径の半分の長さ
一番内側の円の直径が 10 未満にならない範囲でできるだけ多く円を描くとする。

問題 13

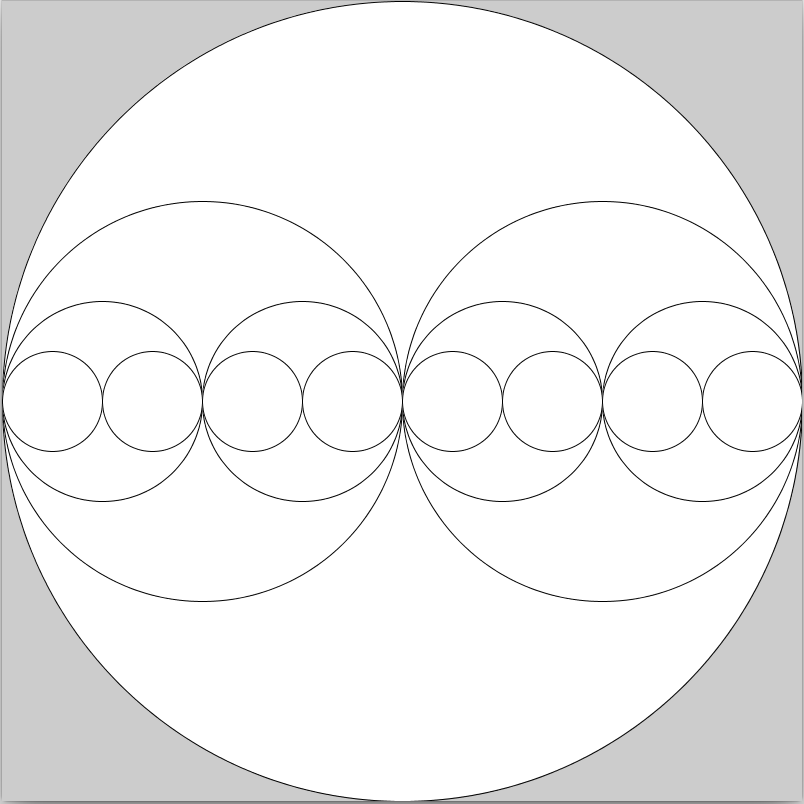
再帰関数を用いて下記の描画結果が得られるプログラムを作成せよ。

Window は正方形，各円は正円
各円の中心の y 座標は，Window の重心の y 座標と同じ
一番外側の円の直径は Window の 1 辺の長さ
外側から n 番目の円の直径は n-1 番目の円の直径の半分の長さ
外側から n 番目の円同士は重ならない
一番内側の円の直径が Window の 1 辺の 1/8 未満にならない範囲でできるだけ多く円を描くことを条件とする。

問題 14

drawRects 関数は引数に x, y, size, minSize をとり、以下の手順で(x, y)を左上の座標とした大きさが size の図形 X を描画する。 size が minSize 以下であれば関数を抜ける

左上の座標が(x + size / 2, y)で一辺が size / 2 の正方形を描画する
左上の座標が(x, y + size / 2)で一辺が size / 2 の正方形を描画する
左上の座標が(x, y)で大きさが size / 2 の図形 X を描画する
左上の座標が(x + size / 2, y + size / 2)で大きさが size / 2 の図形 X を描画する

drawRects を再帰関数として作成し、以下のプログラムを完成させよ。

void setup() {
  size(800, 800);
  fill(0);
  stroke(255);
  background(255);
  noLoop();
}

void draw() {
  drawRects(0, 0, width, 50);
}

問題 15

以下のプログラムは再帰関数によって樹状の図形を描画するプログラムである。 draw 関数内の drawTree 関数の引数を変更し、どのような図形が得られるか確認せよ。また、drawTree 関数の内容について説明せよ。なお、atan2(y, x) は点(0, 0)と(x, y)を端点とした線分が横軸となす角度を返す

void setup() {
  size(800, 800);
  noLoop();
}

void draw() {
  background(255);
  drawTree(width / 2, height, width / 2, height - 120, 12, PI / 6, 0.8);
}

void drawTree(float x0, float y0, float x1, float y1, int remains, float deltaTheta, float scale) {
  if (remains <= 0) {
    return;
  }

  line(x0, y0, x1, y1);
  float theta = atan2(y1 - y0, x1 - x0);
  float d = dist(x0, y0, x1, y1) * scale;
  drawTree(x1, y1, x1 + d * cos(theta + deltaTheta), y1 + d * sin(theta + deltaTheta), remains - 1, deltaTheta, scale);
  drawTree(x1, y1, x1 + d * cos(theta - deltaTheta), y1 + d * sin(theta - deltaTheta), remains - 1, deltaTheta, scale);
}

演習

演習