再帰による図形の描画

次のような、内側の円の半径が 1 つ外側の円の半径の半分となるような同心円を描画することを考えます。

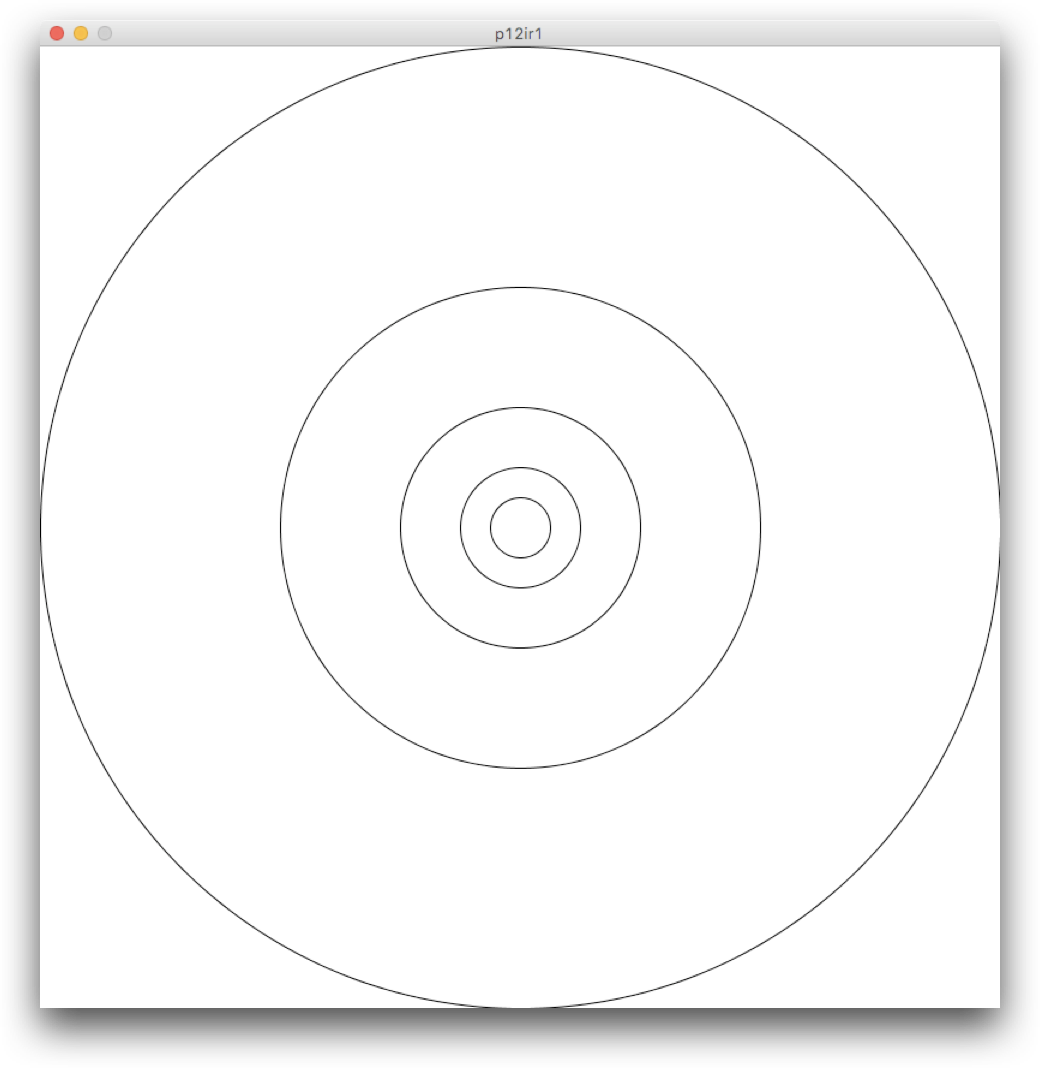
これは、次のように再帰的な処理として記述することができます。

(cx, cy)を中心とした半径rの円の内側に、半径r / 2の自分自身を描画する

ただし再帰の終了条件について考える必要があります。 図形の場合、十分に小さい図形は描画しても画面上はほとんど見えなくなります。 そのため、次のように 2 通りの考え方をとることができます。

終了条件 1：円の半径が一定値（minR）を下回ったとき

void setup() {
  size(800, 800);
  noLoop();
}

void draw() {
  background(255);
  drawCircles(width / 2, height / 2, width / 2, 25);
}

void drawCircles(float cx, float cy, float r, float minR) {
  if (r < minR) {
    return;
  }
  ellipse(cx, cy, 2 * r, 2 * r);
  drawCircles(cx, cy, r / 2, minR);
}

終了条件 2：指定された個数（remains）の円を描き終わったとき

void setup() {
  size(800, 800);
  noLoop();
}

void draw() {
  background(255);
  drawCircles(width / 2, height / 2, width / 2, 5);
}

void drawCircles(float cx, float cy, float r, int remains) {
  if (remains <= 0) {
    return;
  }
  ellipse(cx, cy, 2 * r, 2 * r);
  drawCircles(cx, cy, r / 2, remains - 1);
}

フラクタル図形の描画

図形の「部分」と「全体」が自己相似になっている図形をフラクタルと呼びます。 （自己相似で定義されないフラクタル図形もあります。） 部分と全体が自己相似になっているとは、図形のある部分だけを見たときに、その部分が全体と一致していることを言います。

次の図はコッホ曲線と呼ばれるフラクタル図形の一種を用いて描いたものです。

コッホ曲線は、$(x_0, y_0), (x_1, y_1)$ を結ぶコッホ曲線を描くときに、下図の実線部 4 本の線分に置き換えます。

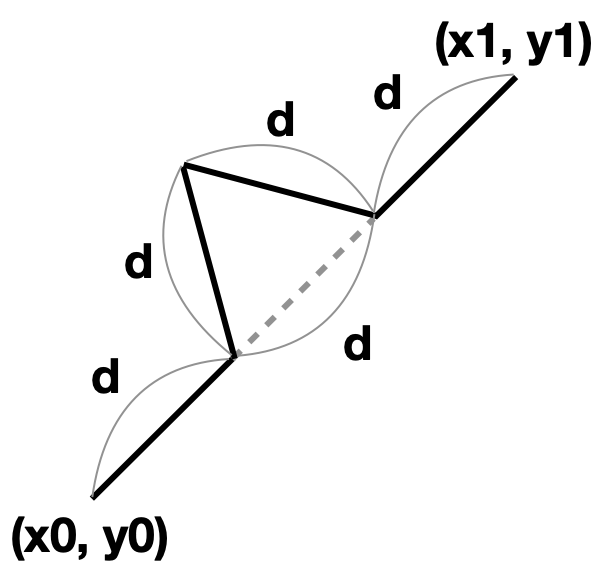
この第 1 段階を実行するプログラムは次の通りです。

void setup() {
  size(400, 400);
  smooth(0);
  background(255);
  noLoop();
}

void draw() {
  drawLines(width / 2, 0, width, height / 2);
  drawLines(width, height / 2, width / 2, height);
  drawLines(width / 2, height, 0, height / 2);
  drawLines(0, height / 2, width / 2, 0);
}

void drawLines(float x0, float y0, float x1, float y1) {
  float p1x = (x1 - x0) / 3 + x0;
  float p1y = (y1 - y0) / 3 + y0;

  float d = dist(x0, y0, x1, y1) / 3;
  float theta = atan2(y1 - y0, x1 - x0) - PI / 3;
  float p2x = p1x + d * cos(theta);
  float p2y = p1y + d * sin(theta);

  float p3x = 2 * (x1 - x0) / 3 + x0;
  float p3y = 2 * (y1 - y0) / 3 + y0;

  line(x0, y0, p1x, p1y);
  line(p1x, p1y, p2x, p2y);
  line(p2x, p2y, p3x, p3y);
  line(p3x, p3y, x1, y1);
}

実行結果は以下ようのになります。

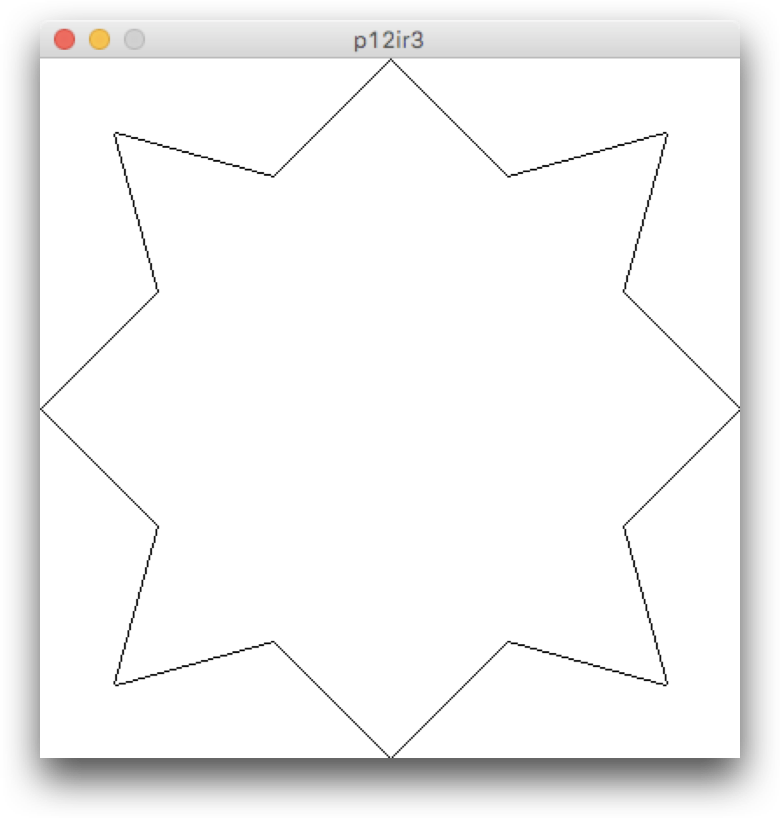
ここで、4 本の線分を自己相似的にコッホ曲線で描くことでコッホ曲線を描くことができます。 コッホ曲線は本来は無限に微小な線分から構成されますが、描画の都合上、描画する最小の長さの線分 minD を定めます。 すなわち、2 点間の距離が minD より大きければ再帰的にコッホ曲線を、そうでなければ 2 点を結ぶ線分を描きます。 プログラムは以下のようになります。

void setup() {
  size(800, 800);
  smooth(0);
  background(255);
  noLoop();
}

void draw() {
  int minD = 10;
  drawKochCurve(width / 2, 0, width, height / 2, minD);
  drawKochCurve(width, height / 2, width / 2, height, minD);
  drawKochCurve(width / 2, height, 0, height / 2, minD);
  drawKochCurve(0, height / 2, width / 2, 0, minD);
}

void drawKochCurve(float x0, float y0, float x1, float y1, int minD) {
  if (dist(x0, y0, x1, y1) < minD) {
    line(x0, y0, x1, y1);
    return;
  }

  float p1x = (x1 - x0) / 3 + x0;
  float p1y = (y1 - y0) / 3 + y0;

  float d = dist(x0, y0, x1, y1) / 3;
  float theta = atan2(y1 - y0, x1 - x0) - PI / 3;
  float p2x = p1x + d * cos(theta);
  float p2y = p1y + d * sin(theta);

  float p3x = 2 * (x1 - x0) / 3 + x0;
  float p3y = 2 * (y1 - y0) / 3 + y0;

  drawKochCurve(x0, y0, p1x, p1y, minD);
  drawKochCurve(p1x, p1y, p2x, p2y, minD);
  drawKochCurve(p2x, p2y, p3x, p3y, minD);
  drawKochCurve(p3x, p3y, x1, y1, minD);
}