処理の抽象化の実用例

関数を用いた処理の抽象化の実用例として、整列アルゴリズムのヒープソートを扱います。 ヒープソートの実装を通じて、単純な関数を組み合わせることで複雑な処理を組み立てることができるという処理の抽象化の効果を学びます。

配列による二分木の表現

ヒープソートは、ヒープというデータ構造を利用します。 ヒープは二分木の一種です。

二分木は下図のように、各頂点が高々 2 個の子を持つ根付き木です。

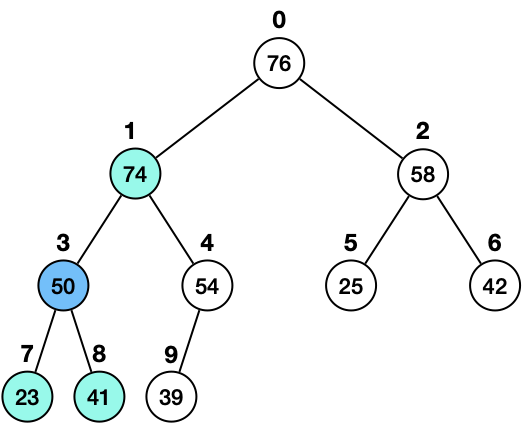
木が $n$ 個の頂点を持つとき、頂点に以下の条件を満たすように番号を振ります。

• 根は 0 番の頂点である
• $i$ 番の頂点 $(0 \leq i < n)$ が左の子を持つとき、左の子は $2i + 1$ 番である
• $i$ 番の頂点 $(0 \leq i < n)$ が右の子を持つとき、右の子は $2i + 2$ 番である

なお、$i$ 番の頂点が根ではないとき、親は $\lfloor \frac{i - 1}{2} \rfloor$ 番となります。

二分木の$n$ 個の頂点に 0 から $n - 1$までの番号を振ることができたので、下図のように二分木を配列で表すことができます。

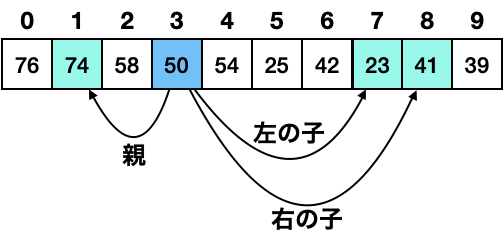
例えば 3 番の頂点の親は 1 番、左の子は 7 番、右の子は 8 番となります。

$i$ 番の頂点の親の番号を $\text{parent}(i)$ 、左の子の番号を $\text{left}(i)$、右の子の番号を $\text{right}(i)$ と表すことにします。

親・子へのアクセス

$i$ 番の頂点に紐付けられた数値を$\text{data}[i]$ と表すことにします。 このとき $i$ 番の頂点の親、左の子、右の子に紐付けられた数値はそれぞれ $\text{data}[\text{parent}(i)]$ 、 $\text{data}[\text{left}(i)]$ 、$\text{data}[\text{right}(i)]$ と表すことができます。

ただし、$i$ 番の頂点に親や子がない場合があります。 その条件を整理すると以下のようになります。

• $i$ 番の頂点が左の子を持つ：$i$ 番の頂点の左の子の番号が $n$ より小さい
• $i$ 番の頂点が右の子を持つ：$i$ 番の頂点の右の子の番号が $n$ より小さい
• $i$ 番の頂点が子を持つ：$i$ 番の頂点が左の子を持つ
• $i$ 番の頂点が根：$i$ が 0 と等しい
• $i$ 番の頂点が親を持つ：$i$ 番の頂点が根ではない

それぞれを以下のように表記することにします。

• $\text{hasLeft}(i, n)$：$n$ 頂点の二分木において、$i$ 番の頂点が左の子を持つとき true, そうでないとき false
• $\text{hasRight}(i, n)$：$n$ 頂点の二分木において、$i$ 番の頂点が右の子を持つとき true, そうでないとき false
• $\text{hasChild}(i, n)$：$n$ 頂点の二分木において、$i$ 番の頂点が子を持つとき true, そうでないとき false
• $\text{isRoot}(i)$：$i$ 番の頂点が根であるとき true, そうでないとき false
• $\text{hasParent}(i)$：$i$ 番の頂点が親を持つとき true, そうでないとき false

ヒープ

全ての頂点において、頂点の値がその頂点の親の値より小さいとき、その二分木をヒープと呼びます。 ヒープの条件をより正確に書くと、根以外の全ての頂点（$i$ 番とする）が $\text{data}[\text{parent}(i)] \geq \text{data}[i]$ を満たすときとなります。

ヒープの定義より、ヒープの根はヒープ内の最大の値を持ちます。

二分木がヒープであるかどうかを以下のように表すことにします。

• $\text{isHeap}(\text{data}, n)$：配列 $\text{data}$ の先頭 $n$ 要素で表される二分木がヒープであるとき true、そうでないとき false

ヒープへのデータの挿入

すでにヒープとなっている二分木に、ヒープの条件を保ったまま新たに一つ頂点を追加する方法を考えます。

追加するデータを新たな頂点としてヒープの末尾に追加します。 新たな頂点の番号を $i$ とし、 $\text{hasParent}(i)$ かつ $\text{data}[i] >= \text{data}[\text{parent}(i)]$ である間、$\text{data}[i]$ と $\text{data}[\text{parent}(i)]$ を入れ替え、$i \leftarrow \text{parent}(i)$ を繰り返せばヒープの条件を保つことができます。 この手続きを$\text{siftup}(\text{data}, i)$ と呼ぶことにします。

下図では、10 要素（0 番から 9 番の頂点）のヒープに新たに 10 番の頂点を追加しています。

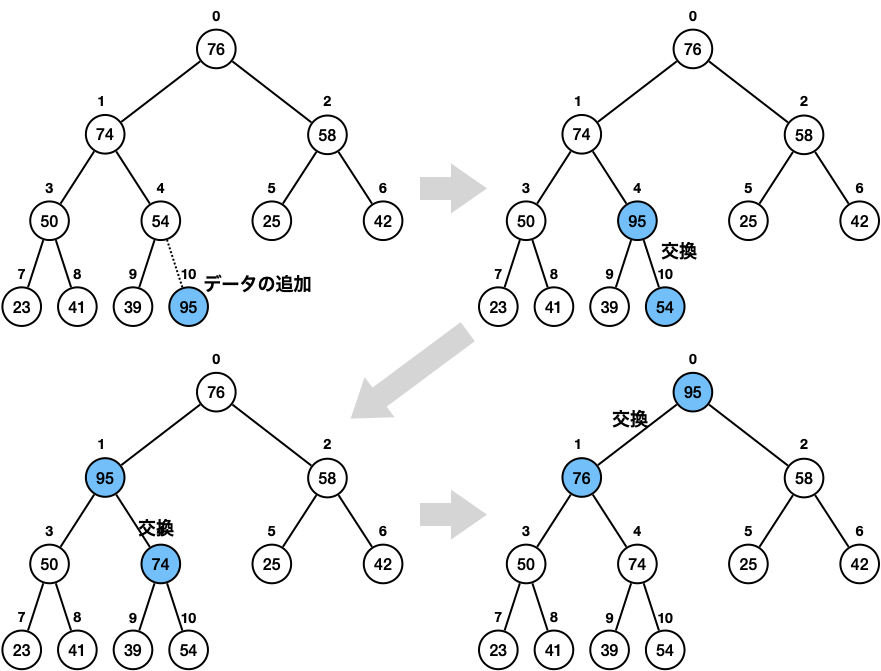
要素数が 1 の二分木はヒープの条件を満たします。 ここから、要素を 1 つずつ順番に$\text{shiftup}$することで配列からヒープを構築できます。

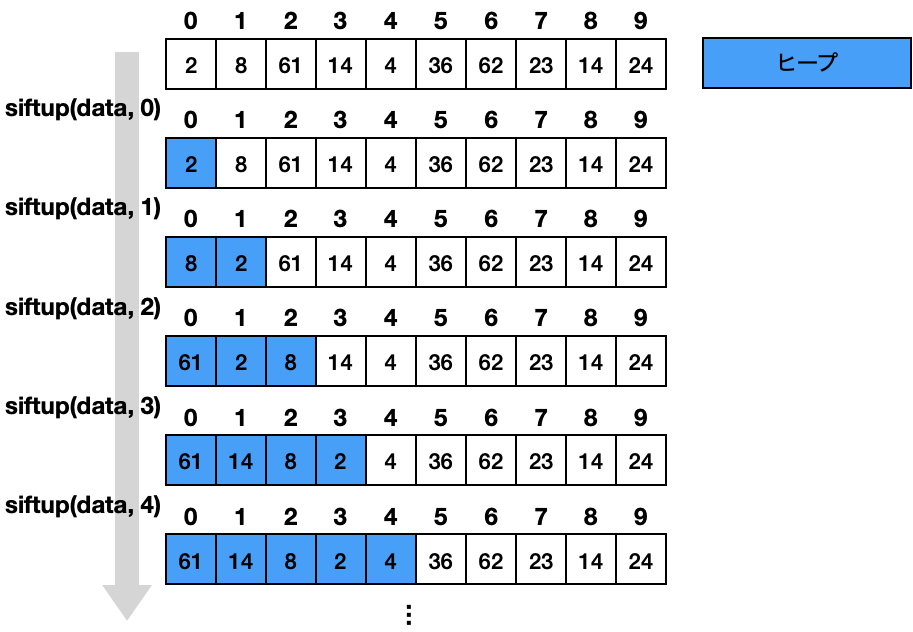
ヒープからのデータの取り出し

ヒープから、値が最大の頂点（根）を取り出し、残りの要素で再度ヒープを構築する方法を考えます。

根を取り出した後、根の位置に残った要素の中の最大値を持ってこなければいけません。 ヒープの要素数が $n$ であるとすると、今ヒープには 0 番から$n - 1$ 番の頂点が含まれています。 0 番の頂点を取り出した後、$n - 1$ 番の頂点を根に仮に持ってきておきます。 根から始まり、現在の頂点の値とその左の子の値と右の子の値の大きい方を入れ替えていけば再度ヒープを構築することができます。

配列 $\text{data}$ の先頭 $n$ 個で表される二分木において、 $i$ の左右の子の値が大きい方を返す処理を $\text{greaterChild}(\text{data}, i, n)$ と表すことにします。 根を $i$ とし、 $\text{hasChild}(i)$ かつ $\text{data}[i] < \text{data}[\text{greaterChild}(\text{data}, i, n)]$ である間、$\text{data}[i]$ と $\text{data}[\text{greaterChild}(\text{data}, i, n)]$ を入れ替え、 $i \leftarrow \text{greaterChild}(\text{data}, i, n)$ を繰り返せばヒープの再構築ができます。 この手続きを $\text{siftdown}(\text{data}, n)$ と呼ぶことにします。

下図は 21 の値を持った根がヒープの条件を満たすように適切な位置へ移動する様子を表しています。

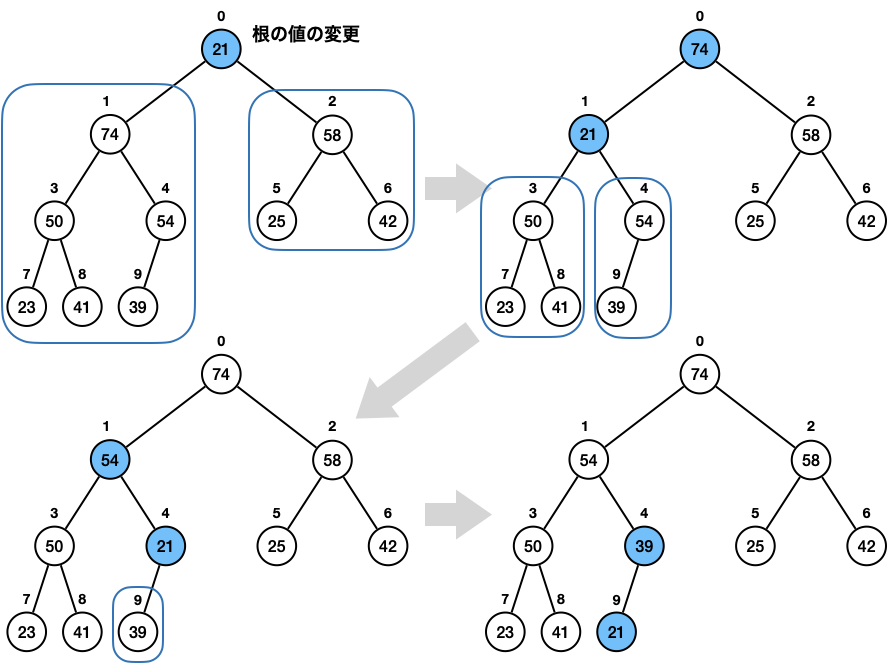
ヒープソート

ヒープから最大値を取り出し、残った要素から再度ヒープを構築する方法がわかりました。 これを利用して、ヒープから順番に最大値を取り出すことで整列を行うアルゴリズムをヒープソートと呼びます。

下図のようにヒープの根と末尾を入れ替えながらヒープの要素数を減らして（ソート済み部分を増やして）いきます。